We don't, in fact, know how machine learning works. With traditional software, we have lines of code and software development assurance systems. When it fails, we can look at the code and understand where and why it failed. Neural networks are closer to the human brain. You can check the software code, but you don't open the pilot's brain to see neurons. So how can we understand a system that produces its own code?"
Traditional handwritten code feels safe and familiar because we are so used to it. It is ubiquitous. On the other hand, mysterious neural networks (NNs) have not inspired much trust so far. However, does that mean that traditional code is a) easier to understand and analyse and b) more predictable and reliable?
Explainability
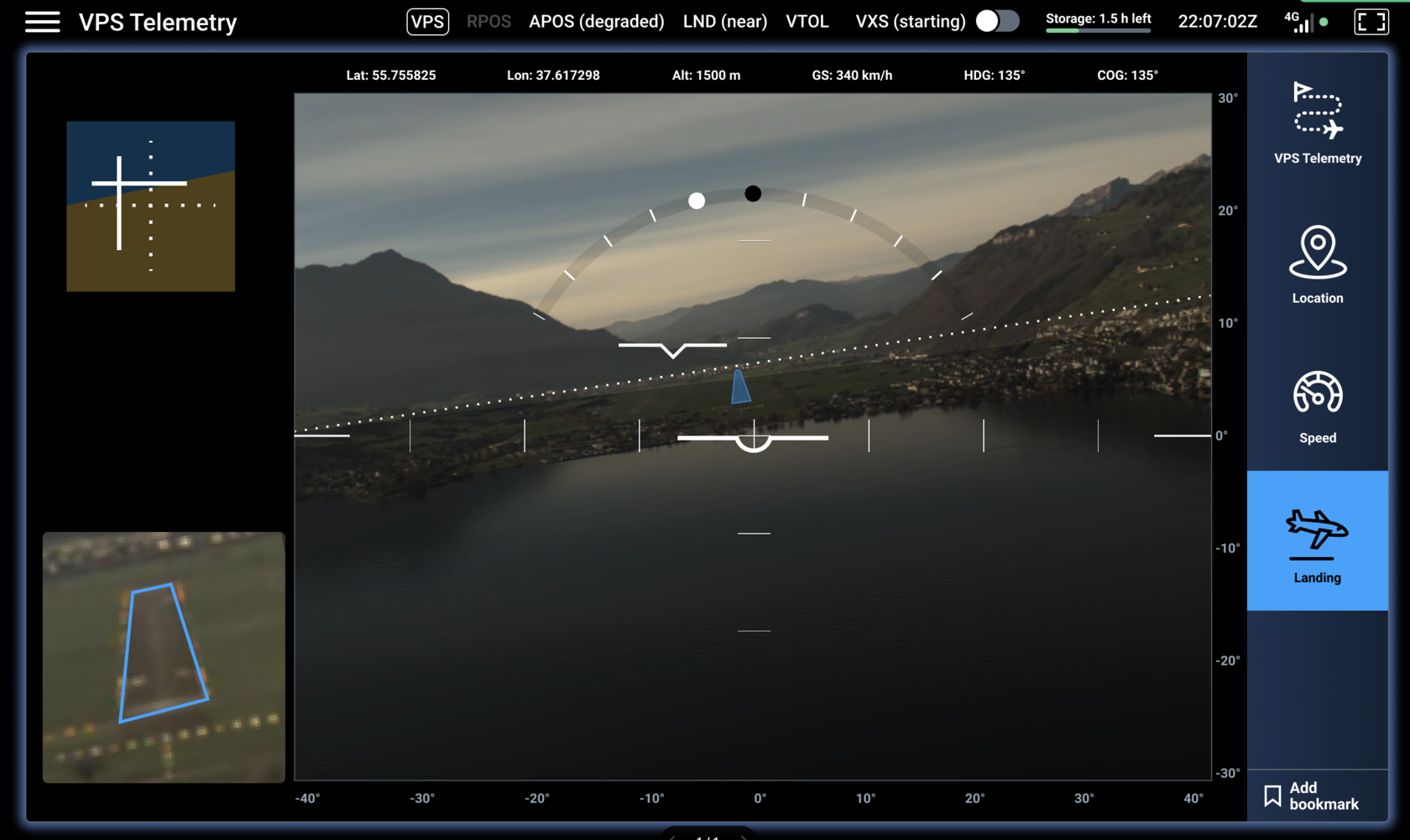
The question of the ‘explainability’ of neural networks has become somewhat of a red herring. If you try to pin it down, the term turns out to be impossible to define. It is impossible to say whether a particular system is understandable or not—based on objective criteria. Of course, the raw contents of a neural network may read as less perceivable than handwritten code. But the very approach of trying to use the raw set of weights of a NN to explain why it does or does not work correctly is the wrong level of explanation. It is like trying to understand a company balance sheet by exploring the ink on the paper on which it is printed.A NN works because it is tuned to a dataset to solve particular problems by performing some computation. For example, in one of our use cases, the NN receives a set of pixels representing an image and draws a box around what it believes to be a runway. Currently, it is accurate 96% of the time on a large, statistically significant set of images. This high level of accuracy is achieved because we know how to train it to properly partition the image into things that look like a runway and not. If it makes a mistake, it may be because a) some data it was trained on was mislabelled, thus learning the wrong pattern from it, or b) the dataset was insufficient and did not cover a particular aspect or case that it is now encountering.
Reliability
DO-178C, the regulatory standard for flight software, establishes the process for writing the code for the software. First, you should very carefully write down what the code is supposed to do. Second, you should very carefully write down how you are going to do that. Third, you should write the code that does that and test it. Finally, you verify the code going up the V-shape to know how well you have coped with the task. However, while the coding standard makes sure that the code is written very neatly, it does not (and cannot) guarantee that the code is correct. In fact, it is implied that you do the work three times and then keep your fingers crossed.Inevitably, no matter how strict a process is imposed, there can always be some unexpected bug because it is very hard to prove that software works correctly—for fundamental mathematical reasons. In computer science, statistics are of little help because the distribution of errors is complex and difficult to guess or compute. If you look at a random piece of code, it’s difficult to develop a metric estimating that there are probably two (or ten) bugs in the code. The halting problem, formulated by Alan Turing, states that it is impossible to design a generalised algorithm that can appropriately say whether an arbitrary given program will ever finish its computation or not. It may perform well in testing conditions, but when applied to much less certain and much more variable real-world data, the time needed to finish the computation may be extremely long—and may even exceed the time left for the existence of the Universe.

The DO-178C says that to be certified for Design Assurance Level B, a piece of software should not fail more than once in 10^7 (10,000,000) hours. The standard also stipulates some procedures related to system engineering and safety analysis and the need to ensure that the requirements are fair, attainable, and truly met by the system. However, of course, no aspect of this strict process guarantees that your system will not fail more than once in 10^7 hours of flight. Incidentally, this is already an exception compared with all the other systems in an aircraft. Specifically, manufacturers put any structural or engine part on the test bench in the lab. It will then be hit 50,000 times to establish that the mean period before a failure is 40,000 hits. After that, the safety certification will prescribe that the particular part be replaced after taking, say, 30,000 hits.

Yet, it is impossible to follow the same procedure with a written code. In the lab, we want to see zero bugs, but we do not (and cannot) know the statistical distribution of them. So, when a bug is found, it is normally during production. There is then an intense process of ‘Ensuring Continued Airworthiness’, and after the bug is fixed, we go back to ‘pretending’ the code is fault-free again.However, statistics is fully applicable to machine-learned programs. With them, we can actually guarantee that 999 times out of 1000, or maybe 96 out of 100 times, if we show our system an image, it will adequately recognise a runway on it. Those programs may look complicated, but their structure is, in fact, straightforward. And while neural networks are not free of faults, the expected failure rate is bound by mathematical theorems—based on the assumption of independent sampling.Furthermore, as mentioned above, the NN correctly detects a target in a single image with a probability of 96%, but in a flight, it continues to process frames from the next points in the sky for some time. Thus, the immediately subsequent images are quite similar, and the likelihood of a failure is thus correlated. But with multiple pictures and a properly constructed system, we have multiple independent chances to get it right. Therefore, the probability of malfunction can be reduced to a sufficiently low level—and we can get stronger guarantees of performance than with classical software. (Remember: it is almost impossible to predict where errors will appear.) So, ironically, with this allegedly ill-understood ‘black box’ magic, once we implement it properly, we may end up with systems that are provably safer than any so-called handcrafted code.




